Les parieurs cherchent souvent des méthodes pour prédire les scores des matchs de football. La loi de Poisson est un outil mathématique simple et puissant qui peut aider à estimer les probabilités de différents scores dans un match. Cet article pédagogique, destiné aux débutants, explique de manière claire ce qu’est la loi de Poisson et comment l’utiliser pour les paris footballistiques. Nous verrons d’abord le principe mathématique de cette distribution (sans effrayer ceux qui sont « allergiques » aux maths), puis nous montrerons concrètement comment l’appliquer pour estimer les chances de chaque score exact dans un match. Un exemple pas à pas avec deux équipes illustrera le calcul des probabilités de score. Enfin, nous conclurons par quelques conseils pratiques, notamment sur les limites de cette méthode (hypothèses d’indépendance, absence de prise en compte de certains facteurs, etc.), afin de l’utiliser à bon escient.

Comprendre la loi de Poisson

La loi de Poisson est une loi de probabilité discrète qui donne la probabilité qu’un événement se produise un certain nombre de fois dans un intervalle de temps fixe, en se basant uniquement sur le nombre moyen d’occurrences observé (appelé λ, lambda) et en supposant que ces événements se produisent de façon indépendante les uns des autres. Autrement dit, si l’on connaît la fréquence moyenne d’un événement, la loi de Poisson permet d’estimer la probabilité d’en voir exactement 0, 1, 2, 3, … occurrences sur une période donnée.

Dans notre contexte du football, l’événement en question est “marquer un but” et l’intervalle de temps est le match (90 minutes). Si une équipe marque en moyenne λ buts par match, la loi de Poisson permet de calculer la probabilité qu’elle marque exactement k buts dans un match. La formule mathématique s’écrit :

P(X=k)=λk⋅e−λk!,P(X = k) = \frac{\lambda^k \cdot e^{-\lambda}}{k!},P(X=k)=k!λk⋅e−λ​,

où λ est le nombre moyen de buts (la moyenne attendue), k! désigne la factorielle de k (par exemple 3! = 3×2×1 = 6), et e est la base des logarithmes naturels (≈ 2,71828). Ne vous laissez pas intimider par cette formule : elle est moins compliquée qu’il n’y paraît. Elle sert simplement à convertir une moyenne en une distribution de probabilités sur tous les nombres de buts possibles.

Par exemple, si une équipe a en moyenne λ = 1,7 buts par match, la loi de Poisson prévoit qu’elle a environ 18 % de chances de ne marquer aucun but, 31 % de chances de marquer exactement un but, 26 % de chances d’en marquer deux, 15 % de chances d’en marquer trois, etc. On voit que même une équipe avec 1,7 but en moyenne a une probabilité non négligeable de finir muette (0 but) lors d’un match donné, et des chances décroissantes de marquer de nombreux buts. Ce principe a été découvert par le mathématicien français Siméon Denis Poisson au 19e siècle, d’où le nom de la loi. Aujourd’hui, cette distribution est largement utilisée en statistiques et en sciences, et s’est invitée dans le domaine des paris sportifs pour modéliser le nombre de buts marqués en football.

Utiliser la loi de Poisson pour prédire un score de foot

Sachant ce qu’exprime la loi de Poisson, comment l’utiliser concrètement pour estimer le score probable d’un match de football ? En pratique, les parieurs analytiques s’en servent pour transformer des données de performance en probabilités de scores exacts. L’idée générale est la suivante : on estime d’abord combien de buts chaque équipe est susceptible de marquer en moyenne dans le match (ses buts “attendus”), puis on applique la loi de Poisson pour obtenir la distribution de probabilités des buts de chaque équipe, et enfin on combine ces distributions pour calculer les probabilités de chaque score possible.

En résumé, on peut décomposer l’utilisation de la loi de Poisson en trois étapes principales :

1. Estimer le nombre de buts moyen de chaque équipe pour le match. C’est la valeur de λ pour chaque équipe (parfois noté μ). Cette estimation se base sur les données historiques et les caractéristiques des équipes. Concrètement, on peut calculer la moyenne de buts marqués par l’équipe A et la moyenne de buts encaissés par l’équipe B, puis en déduire le nombre de buts attendus pour A face à B (on fait de même pour l’équipe B face à A). On tient compte éventuellement de l’avantage à domicile et de la forme offensive/défensive des deux côtés. Par exemple, si l’équipe A a une attaque très performante et que l’équipe B défend mal, on s’attendra à un λ élevé pour A. À l’inverse, une équipe peu prolifique face à une défense solide donnera un λ plus faible. Il est important de choisir une période de données représentative pour ces moyennes : ni trop longue (pour ne pas inclure des performances trop anciennes qui ne reflètent plus le niveau actuel), ni trop courte (pour éviter que quelques matchs exceptionnels faussent la moyenne).
   
   
2. Calculer la distribution de probabilités de buts pour chaque équipe. Une fois les moyennes estimées (par exemple λ_A pour l’équipe A et λ_B pour l’équipe B), on applique la formule de Poisson pour obtenir la probabilité que chaque équipe marque 0, 1, 2, 3, … buts. On obtient ainsi deux distributions distinctes : l’une pour le nombre de buts de A, l’autre pour le nombre de buts de B. Chaque distribution doit totaliser 100 % sur l’ensemble des possibilités (par exemple la somme des probabilités que A marque 0,1,2,3… buts = 100%). En pratique, on peut s’arrêter à 4 ou 5 buts car au-delà les probabilités deviennent très faibles. (Il existe des calculatrices en ligne qui peuvent effectuer ces calculs automatiquement à partir de λ, ce qui évite de le faire à la main.)
   
   
3. Déduire les probabilités de chaque score exact du match. Si l’on fait l’hypothèse (simplificatrice) que les performances offensives des deux équipes sont indépendantes l’une de l’autre, on peut combiner les deux distributions de Poisson pour obtenir la probabilité conjointe d’un score particulier. En termes simples, la probabilité que “A marque i buts et B marque j buts” est le produit : P(A=i et B=j)=P(A=i)×P(B=j)P(A=i \text{ et } B=j) = P(A=i) \times P(B=j)P(A=i et B=j)=P(A=i)×P(B=j). Par exemple, si A a 30 % de chance de marquer 2 buts et B a 10 % de chance d’en marquer 1, alors la probabilité d’un score 2-1 est 0,30 × 0,10 = 0,03 (soit 3 %). On peut faire ce calcul pour chaque combinaison de buts afin d’obtenir la répartition complète des scores possibles. Cela permet d’identifier le score le plus probable du match, mais aussi la probabilité de n’importe quel score exact (utile pour les paris de type “score exact”), ou encore de déduire la probabilité d’une victoire, d’un match nul ou d’une défaite (en additionnant les probabilités de tous les scores donnant ce résultat).

Exemple pratique : Illustrons ces étapes avec un cas simple. Supposons un match entre Équipe A et Équipe B. D’après les statistiques et la forme du moment, on estime que l’Équipe A marquera en moyenne 1,6 but (λ_A = 1,6) et que l’Équipe B marquera en moyenne 0,8 but (λ_B = 0,8) lors de ce match. Ce sont nos deux valeurs de départ.

• Étape 2: Calculons les probabilités de buts pour chacune. Pour l’Équipe A (λ_A = 1,6) :
  • P(A marque 0 but) = e−1,6×1,600!e^{-1,6} \times \frac{1,6^0}{0!}e−1,6×0!1,60​ ≈ 20 %
  • P(A marque 1 but) = e−1,6×1,611!e^{-1,6} \times \frac{1,6^1}{1!}e−1,6×1!1,61​ ≈ 32 %
  • P(A marque 2 buts) = e−1,6×1,622!e^{-1,6} \times \frac{1,6^2}{2!}e−1,6×2!1,62​ ≈ 26 %
  • P(A marque 3 buts) = e−1,6×1,633!e^{-1,6} \times \frac{1,6^3}{3!}e−1,6×3!1,63​ ≈ 14 %
  • P(A marque 4 buts ou plus) = (très faible, < 5 % au total)
  De même, pour l’Équipe B (λ_B = 0,8) :
  • P(B marque 0 but) = e−0,8×0,800!e^{-0,8} \times \frac{0,8^0}{0!}e−0,8×0!0,80​ ≈ 45 %
  • P(B marque 1 but) = e−0,8×0,811!e^{-0,8} \times \frac{0,8^1}{1!}e−0,8×1!0,81​ ≈ 36 %
  • P(B marque 2 buts) = e−0,8×0,822!e^{-0,8} \times \frac{0,8^2}{2!}e−0,8×2!0,82​ ≈ 14 %
  • P(B marque 3 buts ou plus) = (très faible, ~5 % ou moins en cumulé)

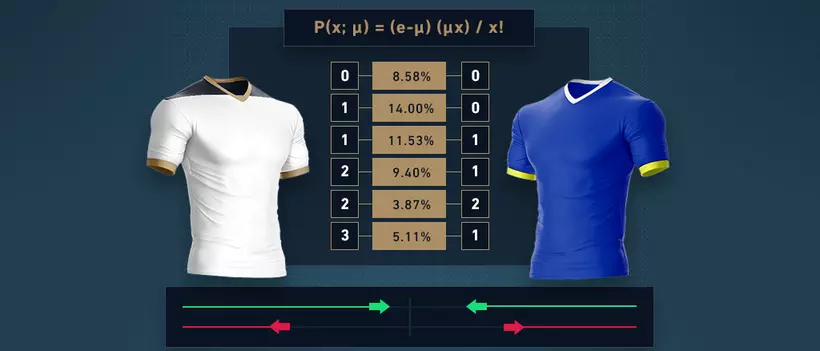
Illustration : Le graphique ci-dessus montre la distribution de Poisson des buts marqués pour nos deux équipes fictives. En jaune l’Équipe A (moyenne 1,6), en orange l’Équipe B (moyenne 0,8). On observe que l’Équipe A a la plus grande probabilité de marquer 1 but (barre jaune la plus haute à 1, soit ~32 %), et possède une probabilité significative de marquer 2 buts (~26 %). En revanche, l’Équipe B a la probabilité la plus élevée de rester à 0 but (barre orange à 0, ~45 %), traduisant une attaque plus faible. Les chances que B marque 1 but sont plus modestes (~36 %) et celles de marquer 2 buts ou plus deviennent assez faibles. Ces distributions individuelles de buts serviront à calculer les probabilités de chaque score exact du match.

• Étape 3: Maintenant, combinons ces résultats pour estimer les probabilités de score exact. Chaque score possible (A vs B) a pour probabilité le produit de la probabilité que A marque ce nombre de buts par la probabilité que B marque ce nombre de buts.
  Par exemple, pour le score 1-0 (A marque 1, B marque 0) :
  P(score 1-0)=P(A=1)×P(B=0)≈0,32×0,45=0,144P(\text{score 1-0}) = P(A=1) \times P(B=0) \approx 0,32 \times 0,45 = 0,144P(score 1-0)=P(A=1)×P(B=0)≈0,32×0,45=0,144, soit 14,4 % de chances.
  Pour le score 1-1 (un but de chaque côté) :
  P(score 1-1)=P(A=1)×P(B=1)≈0,32×0,36=0,115P(\text{score 1-1}) = P(A=1) \times P(B=1) \approx 0,32 \times 0,36 = 0,115P(score 1-1)=P(A=1)×P(B=1)≈0,32×0,36=0,115, soit 11,5 % de chances.
  
  On peut faire de même pour d’autres combinaisons : 2-0 (A 2 buts, B 0) ≈ 11,6 %, 2-1 ≈ 9,3 %, 0-0 ≈ 9 %, 0-1 ≈ 7,3 %, etc. D’après ces calculs, le score le plus probable dans cet exemple serait 1-0 en faveur de l’Équipe A, avec environ 14 % de probabilité. Cela reste une probabilité relativement faible (seulement 1 chance sur 7 environ) – ce qui signifie qu’il est loin d’être garanti, mais c’est le score « favori » d’un point de vue statistique.

En connaissant ainsi la probabilité estimée de chaque score, un parieur peut comparer ces chiffres aux cotes offertes par les bookmakers. Si, par exemple, le score 1-0 est donné à une cote équivalente à seulement 10 % de probabilité par le bookmaker alors que notre modèle le voit à 14 %, cela peut révéler un pari de valeur (value bet). De même, on pourrait additionner les probabilités de tous les scores où A gagne, afin d’estimer la probabilité que l’Équipe A remporte le match, puis comparer avec la probabilité implicite de la cote de victoire de A. Ce type d’analyse aide à déceler des décalages éventuels entre les attentes statistiques et les cotes du marché, et donc à orienter ses paris de façon plus éclairée.

Limites de la méthode et conseils pratiques

Comme tout modèle, l’utilisation de la loi de Poisson en paris sportifs a des limites à connaître. Voici quelques points de vigilance et conseils pratiques pour bien utiliser cette approche :

• Indépendance des événements non garantie – Le modèle de Poisson suppose que les buts sont indépendants (tant chaque but marqué par une équipe au fil du temps que les buts des deux équipes entre eux). En réalité, au football, les événements ne sont pas tout à fait indépendants. Par exemple, si une équipe prend l’avantage 3-0, le match peut changer de physionomie (l’adversaire attaquera à outrance ou baissera les bras, le leader gérera son avance, etc.), ce qui affecte le rythme des buts. De même, les nombres de buts des deux équipes peuvent être corrélés : un match ouvert verra souvent les deux équipes marquer plus que la moyenne, tandis qu’un match fermé les verra marquer moins. La méthode de Poisson classique ne tient pas compte de ces corrélations puisqu’elle traite les deux équipes séparément et multiplie les probabilités. Il faut garder en tête que l’indépendance est une hypothèse simplificatrice – souvent raisonnable sur une large échelle, mais pas toujours vérifiée dans un cas particulier.
  
• Pas de prise en compte des facteurs contextuels – La distribution de Poisson se base uniquement sur une moyenne de buts. Elle ignore complètement le contexte du match et les facteurs extérieurs. Or, de nombreux éléments peuvent influencer le nombre de buts : l’absence d’un joueur clé (un buteur en moins ou un défenseur important blessé), le style de jeu des équipes, l’importance de l’enjeu (un match de coupe peut être plus serré qu’un match amical), les conditions météorologiques, l’état du terrain, etc. Par exemple, si l’attaquant vedette de l’équipe A est forfait, l’estimation de 1,6 but de moyenne devient sans doute trop élevée – le modèle Poisson pur n’ajustera pas cela tout seul.
  Conseil : il faut toujours ajuster ou au moins remettre en question les moyennes de buts λ à l’aune des dernières informations (composition des équipes, dynamique récente, conditions particulières). La loi de Poisson ne doit pas être utilisée de manière aveugle sans réflexion sur le contexte.
  
• Mises à jour et évolutions des équipes – Relié au point précédent, le modèle est aussi aussi bon que les données que vous lui fournissez. Si vous utilisez des statistiques trop anciennes ou non représentatives, les moyennes de buts calculées seront trompeuses. Les équipes de football évoluent : un changement d’entraîneur, une nouvelle recrue offensive, une série de matchs sans marquer… tout cela peut faire bouger la moyenne de buts marqués/encaissés. La loi de Poisson, basée sur l’historique global, ne voit pas ces évolutions. Il est donc judicieux de choisir avec soin la période de référence pour calculer les λ, et de mettre à jour régulièrement ces valeurs en fonction des performances récentes.
  
• Compétences du bookmaker et marge incluse – Enfin, n’oublions pas que les bookmakers connaissent très bien ces modèles statistiques. Sur les grands championnats, ils disposent d’analystes et d’algorithmes sophistiqués qui intègrent la loi de Poisson (et bien d’autres facteurs) pour fixer leurs cotes. De plus, les cotes incluent une marge pour le bookmaker. Ainsi, même si votre modèle Poisson prédit correctement une probabilité, la cote offerte sera généralement ajustée en dessous de la “vraie” probabilité pour garantir la marge du bookmaker. En pratique, cela signifie que trouver des paris de valeur avec la seule loi de Poisson devient difficile sur les compétitions très suivies où le marché est efficient.
  Conseil : utilisez la loi de Poisson comme outil d’analyse pour dégager une tendance ou une base de travail, mais ne pariez pas automatiquement tout ce qu’elle suggère. Combinez-la avec votre connaissance du sport, et cherchez des situations spécifiques (petits championnats, contextes particuliers) où le modèle Poisson pourrait avoir une longueur d’avance sur les cotes proposées.

En conclusion, la loi de Poisson est un modèle simple et instructif pour prédire les scores en football de manière probabiliste. Elle permet de transformer une intuition ou des statistiques de buts en probabilités chiffrées, ce qui aide à mieux comprendre les cotes et la logique derrière les paris sur les scores exacts ou les over/under (plus ou moins X buts). C’est un outil particulièrement utile pour les parieurs débutants souhaitant adopter une approche plus mathématique sans plonger dans des formules trop complexes. Toutefois, il faut l’appliquer avec discernement : gardez à l’esprit ses hypothèses (indépendance, régularité du taux de buts) et ses limites, et complétez-la par une analyse qualitative du match. Avec cette combinaison de statistique et de bon sens sportif, vous serez en meilleure position pour évaluer les probabilités d’un match et, peut-être, dénicher des paris gagnants sur le long terme. Bon pari

Recommandation

Pour ceux qui veulent aller plus loin, nous vous invitons à consulter cet article de Pinnacle.